Floating point Arithmetic-1

19 February 2021 - 4 mins read time
Tags: Language fundamentals floating point

A brief introduction on Data Representation inside computers

Data representation generally refers to the form in which data is stored, processed in a computing device and transmitted across computing devices. Data is stored, processed and transmitted in terms of 0’s and 1’s only. Data representation is machine dependent and depends on the architectural design of the computer.

Generally we have two types of data formats:

• Fixed point data formats
• Floating point data formats

The below flowchart demonstrates the same in brief:

Floating point Arithmetic

• Representation of very large numbers like 732000000000 or very small fraction like 0.000000000000000000326 of data consumes more memory space if we follow the norms from fixed-point data formats.
• To represent the large and small fraction of data within a less storage space, floating point format is used.

• General format of floating point data is:

  $\pm Mantissa \times Base^{\pm exponent}$

• In floating-point representation, normalization concept is used to represent the data in uniform structure.

  $\pm validDigit.fraction \times Base^{\pm exponent}$

• In the computer system, data is always stored in the form of binary therefore Base is 2 by default. Valid bit becomes implicit i.e. 1.Why?because binary number has only 0's and 1's. Also, 0 is not considered a self-weight digit in any radix format. The reason for discussing this point is that since validDigit and Base is implicit, we do not need to waste the memory space to store them.
• Mantissa alignment process is used in the floating point format to adjust the radix point for the given format and thus converting a de-normalized value to normalized one. In this process, right alignment increments the exponent and left alignment decrements the exponent. For example;

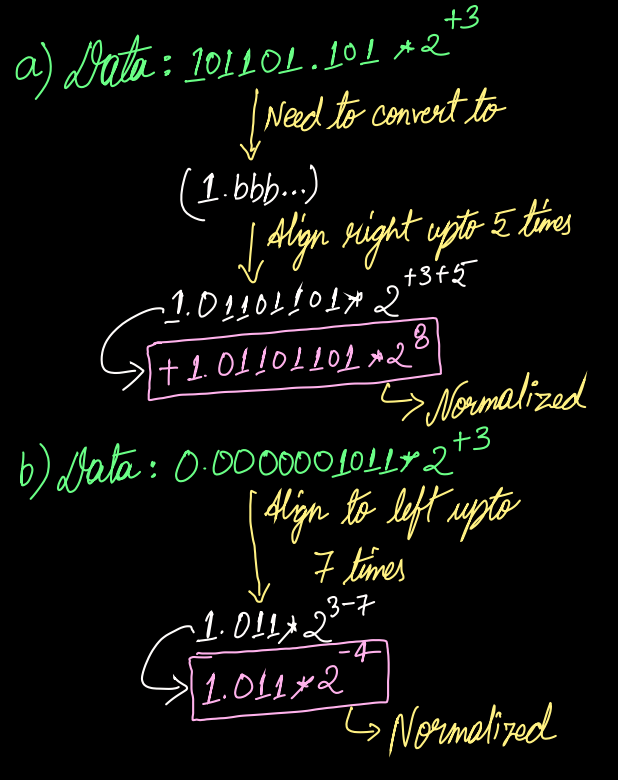
• We store the value in the computer system in normalized form and whenever the value is retrieved, it is reported in de-normalized form.
• When the data is in the normal form; then it is stored in the memory using IEEE formats.

IEEE formats

1. According to IEEE standard 754; there are two kinds formats present:

Floating point data is stored in the memory with three fields of information:

1. Sign field - It used to represent the sign of a data. 0 for positive and 1 for negative.
2. Biased Exponent:
   • In memory, exponent is stored in a biased format rather than the signed format(2’s complement) because Most Significant bit(MSB) is already reserved for the mantissa sign, therefore 2’s complement exponent is not possible to represent the negative exponent.

   • Generally,

     BIASED EXPONENT = ACTUAL EXPONENT + BIAS

   • Bias is maximum possible positive exponent which depends on the format. Biased Exponent field or BEField is discussed below.

     $+2^{n - 1} - 1, n = BEFieldSize$

   • Below is the concept of preserving the sign of an exponent.

       if BiasedExponent > Bias
         then ActualExponent = "Positive"
       else
         ActualExponent = "Negative"
     

   • ExcessBias is another type of Bias where the Bias chosen is the center of the exponent range i.e.

     $\frac{2^n}{2}, n = BEFieldSize$

3. Mantissa Field: It is used to represent the fraction.In memory, fraction is always stored in the normalized mantissa format. i.e. 1.bbbbb where b is either 0 or 1.

In the next post, I’ll try to share my learning on range of floating point number, special values used in floating point numbers and overflow and underflow conditions.