Hilbert's Grand Hotel Paradox
Since, the time I was introduced to discrete mathematics and the applications which it provides to Computer Science; I have developed a stronger affinity towards it. One of the things which fascinates me the most are paradoxes and logical inconsistensies which challenges my mind to think further. Paradoxes are statements or proposition which are logically acceptable through reasoning but lead to a conclusions that seems unacceptable. In general terms, paradoxes are self-contradictory propositions or statements. Here let us discuss a paradox, which is very famous and will also cement our understanding on countably infinite sets. Before diving directly on the paradox let us first get a primer on Sets and their cardinality.
A short primer on Sets and Cardinality of Sets
Sets are used to group objects together. Often, but not always the objects in a set have similar properties. The relative sizes of infinite sets can be studied by introducing the notion of the size or cardinality of a set. Cardinality refers to the number of objects present inside a set. This term comes from the common usage of the term cardinal numbers as the size of a finite set. Now, the question comes why cardinality is so important and what is its relation with computer science. Well, here comes the concept of computable and uncomputable functions. A function is uncomputable if no computer program can be written to find all its values even with unlimited time and memory. This is one of the reason to know about the cardinality of any set. Now we need to classify the sets based on the cardinality as sshown in the flowchart below.
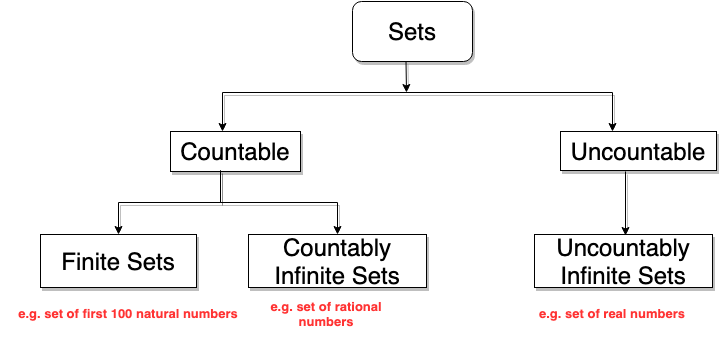
The interest is particularly in countably infinite sets. If we define the countable sets in much broader way, we can say that Countable Sets are sets which are either finite or has the same cardinality as the set of positive integers. When an infinite set S is countable, we denote the cardinality of S by ℵ0 which is referred as aleph-null or aleph-naught.
Now The Paradox…
Hilbert’s Grand Hotel Paradox shows something impossible with finite sets may be possible with infinite sets. The paradox says, “There is always a room for the new guest in Hilbert’s grand hotel even when all the rooms are pre-occupied.” Let us understand this paradox intuitively through a story.
Imagine a hotel with infinite number of rooms and a very hardworking night manager. One night the infinite Hotel is completely full; totally booked up with infinite number of guests.
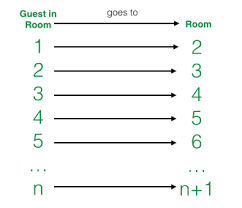
- Case 1: A man walks into the hotel and asks for a room. Now, there is a condition with the night manager. He is very hospitable and do not want to turn down any visitor. So he decides to make room for the new visitor. How? He asks the person from room 1 to shift to room 2, room 2’s person to room 3 and so on as depicted in the image below. Every guest moves from room n to room n + 1. Since, there are infinite number of rooms, there is room for every guest. This leaves room 1 open for the new customer. This process can be repeated for any finite number(k) of new guests.
-
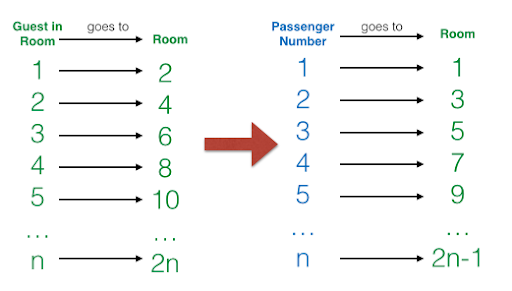
Case 2: Now, an infinetely large bus with countably-infinite number of passengers pulls up to rent a room. Now, to arrange the rooms for every passengers, the night manager comes up with the idea of shifting every nth room person to every 2nth room thereby filling only even numbered rooms and emptying the odd numbered rooms. So now we can accomodate the new infinte guests in these odd numbered rooms thereby making the hotel business booming. Maths always works and that’s why it is fun.